슬라이딩 윈도우
배열이나 문자열같은 일련의 데이터를 입력하거나 특정 방식으로 연속적인 해당 데이터의 하위 집합을 찾는 것에 유용함! 규모가 큰 데이터셋에서 데이터의 하위 집합을 추적하는 문제에 매우 유용함

흠 넵 우선 예시로 풀어볼 문제는
첫번째 인자값으로 배열이 들어오며, 두번째 인자값은 number로 배열의 각각의 num만큼의 배열 합계중 가장 큰 합을 구하는 문제
maxSumArrSum([1, 2, 5, 2, 8, 1, 5], 2) -- 10 ( 1+2 , 2+5, 5+2, 2+8, 8+1, 1+5 중에서 가장 큰 합)
maxSumArrSum([], 4) -- null
maxSumArrSum([4, 2, 1, 6], 1) -- 6
function test (arr, num){
let maxNum = 0;
for(let i=0; i<arr.length; i++){
let tempSum = 0;
for(let j=i+1; j<num + i; j++){
tempSum = arr[i] + arr[j];
console.log(arr[i], arr[j])
}
if(tempSum >= maxNum){
maxNum = tempSum;
console.log(maxNum)
}
}
return maxNum;
}
test([1, 2, 5, 2, 8, 1, 5], 2);
우선 저는 이중for문으로 문제를 해결하였습니다.. ;-;
배열이 짧을 경우에는 중첩 루프를 사용하는 것이 큰 문제가 되진 않겠지만, 만약 배열의 길이가 방대하다면...
그리고 만약 더해야하는 num의 갯수가 10, 40, 50이라면...
i는 50개의 값을 계속해서 더하고 i의 값이 2로 넘어갔을때 또다서 2,3,4,5...52까지 하나씩 구해줘야하게 됩니다.. (;;;;)

이런 경우에 효과적으로 사용할 수 있는 알고리즘이 바로 슬라이딩 윈도우 기법!
function test (arr, num){
let maxSum = 0;
let tempSum = 0;
if(arr.length < num) return null;
for(let i=0; i<num; i++){
tempSum += arr[i];
}
maxSum = tempSum;
for(let i=num; i<arr.length; i++){
tempSum = tempSum - arr[i-num] + arr[i];
maxSum = Math.max(maxSum, tempSum);
}
return maxSum;
}
test([1, 2, 5, 2, 8, 1, 5], 2);
위의 코드에 for문이 두번 들어가지만 O(n)의 시간복잡도로 보실 수 있고 첫번째 for문에서 num 까지의 길이가 합을 먼저 계산해서 변수에 저장해둡니다.
그리고 두번째 for문에서는 i의 위치를 num으로 잡아줍니다. 그리고 현재 tempSum에 들어가 있는 합계에 i의 위치 값을 더해주고, 맨 처음 값을 빼줍니다.
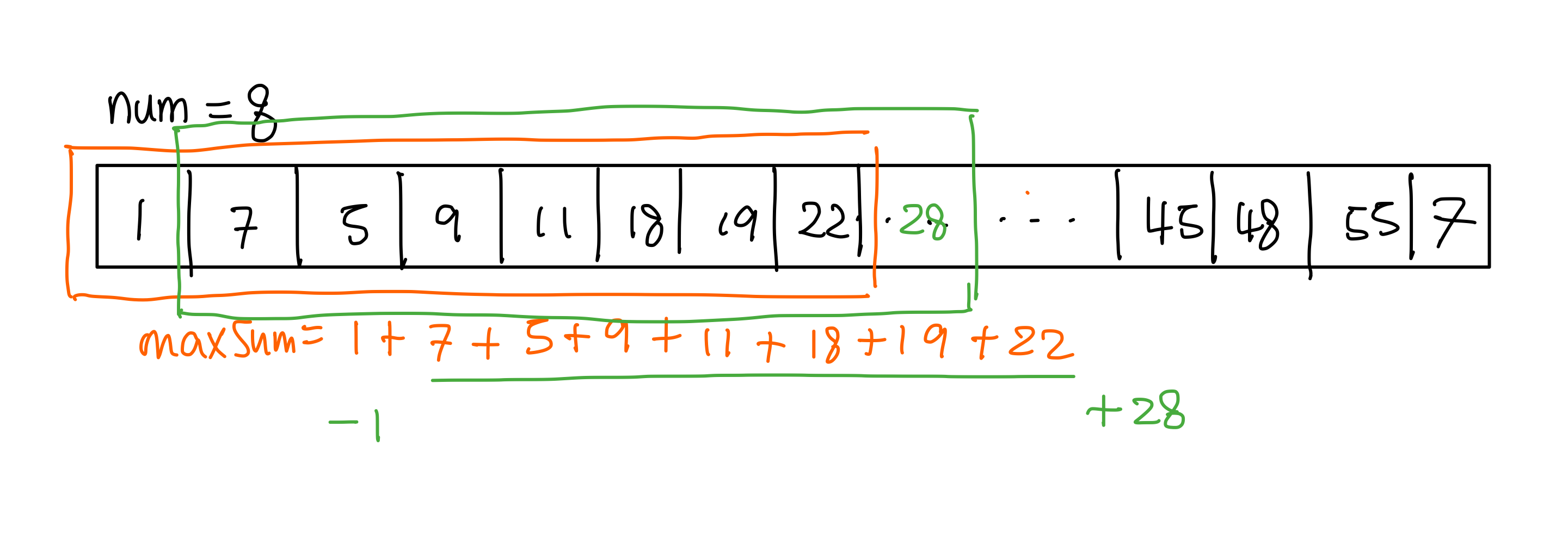
이렇게 슬라이딩 윈도우 기법을 활용하면 매번 모든 인덱스 값을 하나씩 더 해주지 않고 for문안에서 단순하게 빼고 더하기만 해주면 합계를 구할 수 있기 때문에 매우 효과적인 기법이라고 볼수 있네욥!

'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Two Pointers (0) | 2022.07.26 |
|---|---|
| [알고리즘] Frequency Counter Pattern (0) | 2022.07.19 |
| [알고리즘] 배열의 시간복잡도 (0) | 2022.07.13 |
| [알고리즘] 빅오표기법 - 1 (0) | 2022.07.08 |
| [프로그래머스] 자바스크립트 코테 연습 - 4 (feat.reduce함수) (0) | 2022.06.29 |



